# 🔻 Conditional Patterns in Rule 30 and Their Implications on Computational Reducibility
*James K. Wiles | 2023-08-27*
# Problem:
DOES COMPUTING THE NTH CELL OF THE CENTER COLUMN REQUIRE AT LEAST O(N) COMPUTATIONAL EFFORT? [5]
# Abstract:
This research paper explores the emergence of predictable triangle patterns within Rule 30's evolution and examines its potential implications on computational efficiency. By identifying and characterising these patterns, the study seeks to understand scenarios where the standard computational effort might be reduced, albeit conditionally. While the established perception posits an O(N) computational effort for the nth cell of Rule 30, the findings in this paper highlight instances where this might be temporarily bypassed.
# Introduction:
Rule 30, a one-dimensional cellular automaton introduced by Stephen Wolfram, has long been an archetype of complex behaviour arising from simple rules. Its evolution poses intriguing questions on predictability and computational irreducibility [3]. This research aims to shed light on specific patterns that emerge within Rule 30's chaotic behaviour and the potential to predict subsequent evolutions, at least conditionally. By identifying and formalising these patterns, we aim to show that it is possible to compute some nth cells with less than O(N) computation.
# Methodology:
1. **Pattern Recognition:** A rigorous examination of Rule 30's evolution was undertaken to identify recurring patterns [2]. Special attention was given to patterns leading to deterministic behaviour in subsequent rows. Additional attention was given to patterns overlaying the centre column.
2. **Computational Efficiency Analysis:** For each recognized pattern, an evaluation was carried out to determine the potential computational savings. The time complexity in the presence and absence of these patterns was assessed.
3. **Computation and Composition Tools:** Extraction of Rule 30 sequences and validation of thought processes were done using OpenAI’s ChatGPT GPT-4 Code Interpreter August 3 Version.
4. **Validation of Sequences:** Rule 30 sequence validation was done using the Rule 30 Wikipedia entry [4].
# Observations:
1. **The Emergent Triangle Pattern:** When an initiating line, composed exclusively of 3 or more white/blank cells (represented by 0's), is observed, a triangle structure predictably forms. This "emergent triangle," exhibits deterministic formation and evolution. This allows for anticipation of certain cell states within the pattern without processing the preceding cells.
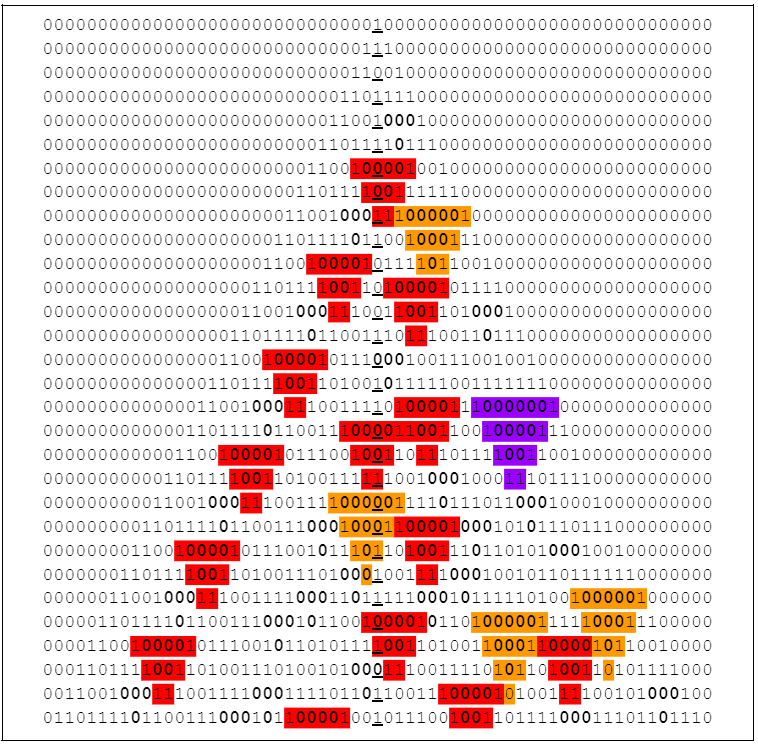
*Rule 30 up to to row 30 showing the emergent triangles of different lengths*
2. Prediction Length: Predicting rows beyond the immediate next iteration becomes feasible for initiating lines with a length greater than 2 cells. The emergent triangle is always enveloped by one additional predictive cell. This cell can be either 1 or 0, determined by whether the initiating line contains an even or odd number of cells.

*Emergent triangles with initiating cell line lengths 3, 4, 5, and 6 respectively*
3. Significant Emergent Pattern: The first non-trivial prediction for the centre column can be found starting from row 7. At this row, an emergent triangle forms from an initiating line with a length of 4 cells, with the centre column situated on the second cell of the initiating line. This configuration allows for the prediction of the centre column's outcome for 2 iterations. A more significant prediction emerges on row 105, offering predictions for 3 iterations.

*Patterns emerging over the centre column on row 7 and row 105 respectively*
4. **Positional Predictability:** For a cell at position _p_ in an initiating line of length _L_ the number of predictable rows _R_:
- If _L_ is odd and the cell is at the centre (i.e., _p = (L+1)/2_), then _R=(L+1)/2_.
- If _L_ is even and the cell occupies one of the two central positions (i.e., _p = L/2_ or _p = (L/2) + 1_), then _R=L/2_ for both positions.
- For other cells, the predictability reduces symmetrically as you move away from the centre. The number of predictable rows, _R_, is calculated as _L/2_ minus the absolute distance of the cell from the closest centre position, plus _1_. The distance from the centre is calculated using _p - (L/2)_.
5. Computational Implications: The emergence of the "emergent triangle" pattern provides instances of O(1) computational complexity for cells within its predictable confines. Beyond these specific patterns, the automaton displays its conventional linear time complexity, O(N).
# Discussion:
1. **Impact on Predictability:** These patterns provide deterministic behaviour windows within Rule 30's otherwise chaotic evolution. It is easy to determine that we have entered one predictable phase of cell evolution given identification of the initiating line.
2. **Existence of Other Patterns:** While this study focused on the emergent triangle, other patterns offering deterministic insights could exist and merit further exploration.
3. **Rule 30 Paradigm Shift:** These observations enrich our understanding of Rule 30, suggesting that deterministic pockets can emerge within broader chaotic contexts.
4. **Relationship to Consciousness:** Creating reliable predictions about future events, and the predictor’s place in and effect on it, is an important requirement for conscious life forms. The ability for a computationally bounded brain to navigate an environment with a greater computation than its own, is achieved with bounded separation from the environment and the processing of environmental inputs using compressed internal representations of objects in the environment [1]. This is related to what we have discovered here in Rule 30:
1. Conscious observer is the iterative observation of the centre column
2. Boundedness is created by the triangle shape separating externalities
3. Universality of life is not possible within Rule 30 due to missing the minimal 3rd dimensionality required for non-ergodicity as there are only two freedoms of movement [*]:
1. Compute the entire line
2. Compute the emergent pattern instead
# Conclusion:
Traditionally, the computation of the nth cell in cellular automata like Rule 30 is viewed through the lens of linear computational effort, represented by O(N). However, our observations and analyses have brought to light specific patterns, notably the emergent triangle, which allow for pockets of predictability within the broader unpredictable structure. In instances where these patterns occur, especially for larger triangles, the computation for certain cells can be achieved in constant time, or O(1), without the need to process every preceding cell.
It's essential to differentiate between the worst-case scenario of computational effort and the actual operations needed under specific conditions. While in many cases, the effort remains linear, our findings demonstrate that, under particular conditions, the computation can be more efficient than previously understood. This challenges the conventional view of a strict O(N) computation for every nth cell and underscores the importance of recognizing and leveraging structures within seemingly chaotic systems.
The nature of Rule 30 and similar cellular automata is complex, intricate, and often unpredictable. Yet, as with many natural systems, pockets of order and predictability exist, waiting to be discovered. Our study serves as a testament to the interplay between order and chaos, and how even in the midst of unpredictability, moments of clarity can shine through, offering avenues for reduced computational effort.
# References:
[1] James Wiles. “Consciousness as a compressed internal model of the environment”. James Wiles Writings, 07 Apr 2021. [https://jameswiles.com/blog/Consciousness-as-a-Compressed-Internal-Model-of-the-Environment.html](https://jameswiles.com/blog/Consciousness-as-a-Compressed-Internal-Model-of-the-Environment.html)
[2] "Live Coding Stream - Hacking Cellular Automata - Wolfram Rule 30 Prize submission" YouTube, Streamed live by James Wiles on 29 Nov 2020.[https://www.youtube.com/live/eSQTBfrHP8k?si=PbjoN1jNsfnhY5n4](https://www.youtube.com/live/eSQTBfrHP8k?si=PbjoN1jNsfnhY5n4)
[3] Stephen Wolfram. A New Kind of Science. Wolfram Media, 2002.[https://www.wolframscience.com/nks/chap-2--the-crucial-experiment/](https://www.wolframscience.com/nks/chap-2--the-crucial-experiment/)
[4] Wikipedia contributors. "Rule 30." Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 18 Aug. 2023. Web. 27 Aug 2023. [https://en.wikipedia.org/w/index.php?title=Rule_30&oldid=1170971344](https://en.wikipedia.org/w/index.php?title=Rule_30&oldid=1170971344)
[5] Stephen Wolfram. "Announcing the Rule 30 Prizes." Stephen Wolfram Writings, 1 Oct 2019. [https://writings.stephenwolfram.com/2019/10/announcing-the-rule-30-prizes/](https://writings.stephenwolfram.com/2019/10/announcing-the-rule-30-prizes/)
# Notes:
Turing completeness could emerge given a third dimension of freedom (three dimensions being the minimal requirement for a non-ergodic universe with quantum states of ambiguous conclusion) by deciding to store the saved computation from consuming the negentropic triangles and applying the energy to travel either left or right out of the centre line. Thus creating computational memory and conditional branching logic.